TiKZ Introductory Guide

Author: Ernesto Martínez García

Tags: 0013 latex tikz

Welcome to this introductory guide to the hard and horrible world of figures in LaTeX. Today we will be learning TiKZ. I personally use Typst+CeTZ for my personal work, but I recently started a PhD in Information Security, and for collaboration and publishing purposes I’m tied to LaTeX. So, I decided to learn TiKZ from the basics and stop copy pasting, hopefully.

First, let me reference two important resources:

Basic environment

Let’s start with how you can start writing a TiKZ figure:

1
2
3
4
5
6
7

\documentclass[crop,tikz]{standalone}

\usepackage{tikz}

\begin{tikzpicture}
	% Tikz Code Here!
\end{tikzpicture}

Now you can compile it with your favorite LaTeX wrapper, hoping it fixes decade-old problems inherent from LaTeX. You can also go and make a coffee in the meantime.

Another way to start a TiKZ drawing environment is inlining it:

1

Lorem \tikz \node[circle,fill=blue] {me}; ipsum

which produces:

What the things inside the TiKZ environment mean will come later.

Just know that you can have a tikzpicture but also inline \tikz.

Paths, draws, fills, and nodes

Let’s study what we can write inside a tikz figure.

The path defines, well, a path:

1
2
3
4
5
6
7

\documentclass[crop,tikz]{standalone}

\usepackage{tikz}

\begin{tikzpicture}
	\path (0,0) -- (1,1) -- (2,2) -- (3,3);
\end{tikzpicture}

You will see that we have not printed anything, there’s no output. That’s because we just defined a path. We just defined a path with a set of coordinates (which we will explain later), but nothing to draw on.

We can instruct TiKZ to please draw the path with \path[draw]:

1
2
3

\begin{tikzpicture}
  \path[draw] (0,0) -- (1,1) -- (2,2) -- (3,3);
\end{tikzpicture}

And now we get our path drawn.

\path[draw] is so used that it can be simplified as \draw! But that’s just an abbreviation, in reality, you are writing a path.

You can also do \path[fill] to fill it with contents instead of drawing the path, let’s see how it works:

1
2
3
4

\begin{tikzpicture}
  \path[fill,blue] (0,0) -- (1,1) -- (1,0) -- (0,0);
  \path[fill,red] (0,0) -- (1,1) -- (0,1) -- (0,0);
\end{tikzpicture}

Now we were able to fill the inside contents of our path with \path[fill]. This is so used that it can be abbreviated as \draw, but that’s still a path!

Another fundamental instruction in TikZ is \node. This one is actually different than a path. Nodes are not paths, are not part of the path either. Rather, they are added to the picture before or after a path has been drawn.

Let’s see it with an example:

1
2
3
4
5

\begin{tikzpicture}
  \node at (0,0) {1};
  \node at (2,2) {2};
  \node at (9,0) {3};
\end{tikzpicture}

See? We placed some content (in our case, numbers) in the TiKZ figure, and these are nodes.

A very useful feature is that we can name our nodes:

1
2
3
4
5

\begin{tikzpicture}
  \node(A) at (0,0) {1};
  \node(B) at (2,2) {2};
  \node(C) at (9,0) {3};
\end{tikzpicture}

Nothing changes in the picture, but now we can reference this coordinates with a path or other functions:

1
2
3
4
5
6

\begin{tikzpicture}
  \node(A) at (0,0) {1};
  \node(B) at (2,2) {2};
  \node(C) at (9,0) {3};
  \draw (A) -- (B) -- (C) -- (A);
\end{tikzpicture}

Nodes are usually shapes (a circle, a rectangle, etc). Nodes can take their shape with the shape= argument. There are three predefined shapes by default, but more can be added with the shapes.multipart tikz library.

Adding the shapes.XXX library via \usetikzlibrary{shapes.XXX} gives many more shapes, see https://tikz.dev/library-shapes.

Let’s put it to use:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

\usetikzlibrary{shapes.geometric}

%...

\begin{tikzpicture}
  \node(A)[shape=circle,fill=green] at (0,0) {1};
  \node(B)[shape=rectangle,fill=blue] at (2,2) {2};
  \node(C)[shape=diamond,fill=yellow] at (9,0) {3};
  \draw (A) -- (B) -- (C) -- (A);
\end{tikzpicture}

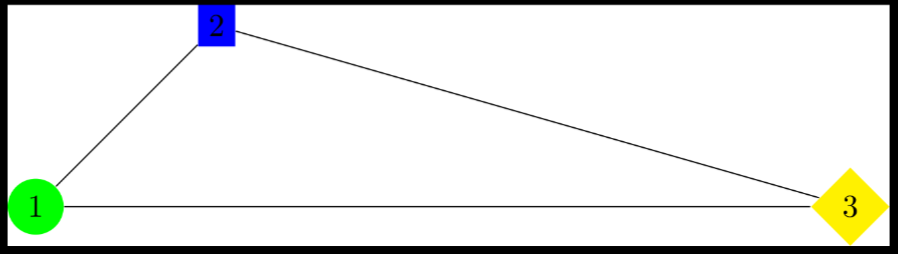
As shapes are very common in nodes, they have some syntactic sugar, if TiKZ doesn’t understand an option passed, it will try to understand it as a shape, thus the following is valid TiKZ and equivalent to the previous snippet:

1
2
3
4
5
6

\begin{tikzpicture}
  \node(A)[circle,fill=green] at (0,0) {1};
  \node(B)[rectangle,fill=blue] at (2,2) {2};
  \node(C)[diamond,fill=yellow] at (9,0) {3};
  \draw (A) -- (B) -- (C) -- (A);
\end{tikzpicture}

Nodes and paths can be mixed, see the following example:

1
2
3

\begin{tikzpicture}
  \draw (0,0) node[circle,fill=green]{1} -- (2,2) node[rectangle,fill=blue]{2} -- (9,0) node[diamond,fill=yellow]{3} -- (0,0);
\end{tikzpicture}

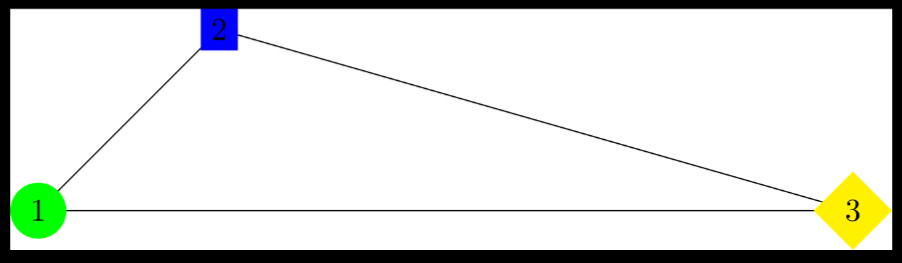
For drawing big figures not mixing paths and nodes might be better for readability, but maybe this is helpful for inline TikZ.

Coordinates

Probably not a mistery for anyone using TiKZ that coordinates exist. We have been using them previously here. But let’s give a proper explanation.

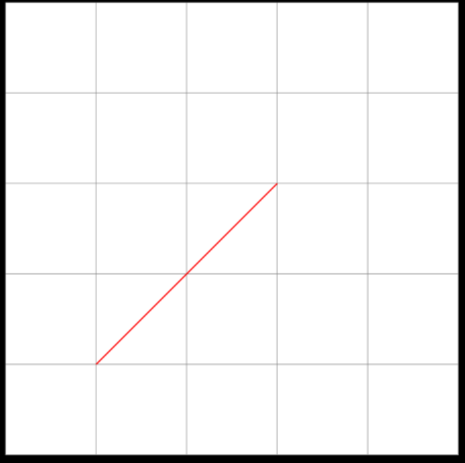
Coordinates are used to specify positions inside the TiKZ canvas, see:

1
2
3
4

\begin{tikzpicture}
  \draw[help lines] (0,0) grid (5,5);
  \draw[red] (1,1) -- (2,2) -- (3,3);
\end{tikzpicture}

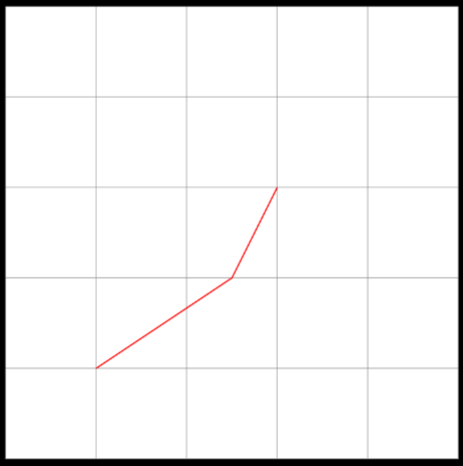
and changing the coordinate reflects a change in our line:

1
2
3
4

\begin{tikzpicture}
  \draw[help lines] (0,0) grid (5,5);
  \draw[red] (1,1) -- (2.5,2) -- (3,3);
\end{tikzpicture}

There’s two ways of specifying the coordinates:

In explicit coordinates, we have to specify the coordinate system used (more on that later). In implicit coordinates, TiKZ (commonly) guesses which one you are using.

There are multiple coordinate systems:

From all this ones, the most important for us will probably be canvas, xyz and node. Maybe * polar if you are smart enough (I’m not).

You can, per coordinate, specify the coordinate system used (this will be an explicit specification!):

1
2
3
4

\begin{tikzpicture}
  \draw[help lines] (0,0) grid (5,5);
  \draw[red] (canvas cs:x=1cm,y=1cm) -- (2.5,2) -- (3,3);
\end{tikzpicture}

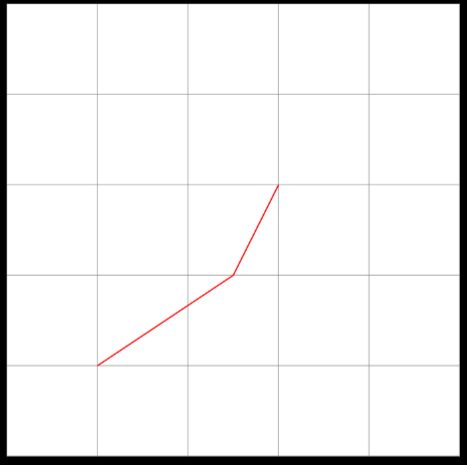
See how we used the canvas coordinate system in the first coordinate explicity, but the others don’t have it? Well, we are mixing explicit and implicit coordinate specifications. TiKZ is guessing the coordinate system of the last two points to be canvas.

Note: canvas cs:x=1cm,y=1cm reads as “canvas coordinate system”, and then the specification. Might be helpful to remember the syntax.

Let’s try the xyz coordinate system:

1
2
3
4
5
6
7
8

\begin{tikzpicture}
  \draw[help lines] (0,0) grid (5,5);
  \draw[red] (1,1,0) -- (2,1,0) -- (2,2,0) -- (1,2,0) -- (1,1,0);
  \draw[blue] (1,1,0) -- (1,1,-1) -- (1,2,-1) -- (1,2,0);
  \draw[green] (2,1,0) -- (2,1,-1) -- (2,2,-1) -- (2,2,0);
  \draw[yellow] (2,1,-1) -- (1,1,-1);
  \draw[orange] (2,2,-1) -- (1,2,-1);
\end{tikzpicture}

Now let’s move to the node coordinate system, which we already used in the past.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

\begin{tikzpicture}
  \draw[help lines] (0,0) grid (5,5);

  \node(A)[draw] at (1,2) {Item 1};
  \node(B)[draw] at (4,1) {Item 2};
  \node(C)[draw] at (4,2) {Item 3};
  \node(D)[draw] at (4,3) {Item 4};

  \path[draw] (node cs:name=A,anchor=east) -- (node cs:name=C,anchor=west);
  \path[draw] (node cs:name=B,anchor=west) -- (2.5,1) |- (A);
  \path[draw] (node cs:name=D,anchor=west) -- (2.5,3) |- (A);
\end{tikzpicture}

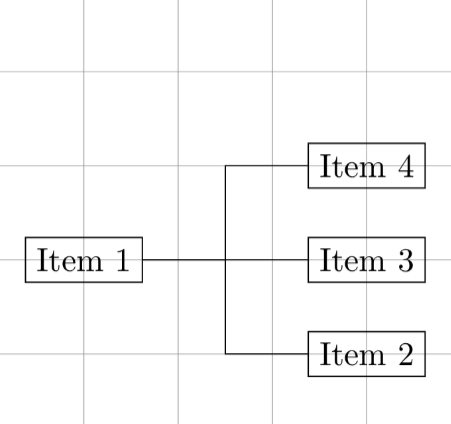
See how we define 4 nodes: A, B, C, D. Then, we reference these nodes as if there were coordinates, that’s called the node coordinate system. We draw lines from A to C, from B to a coordinate and then A, and from D to a coordinate and then A.

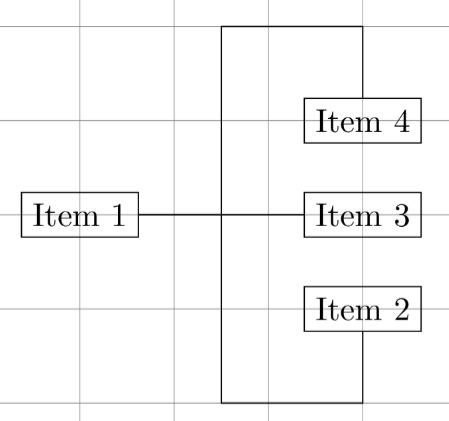
One very important note from here is the anchor option. This represents where the path is being started from in the node.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

\begin{tikzpicture}
  \draw[help lines] (0,-1) grid (5,5);

  \node(A)[draw] at (1,2) {Item 1};
  \node(B)[draw] at (4,1) {Item 2};
  \node(C)[draw] at (4,2) {Item 3};
  \node(D)[draw] at (4,3) {Item 4};

  \path[draw] (A) -- (C);


  \path[draw] (node cs:name=D,anchor=north) -- (4,4) |- (2.5,4) |- (A);
  \path[draw] (node cs:name=B,anchor=south) -- (4,0) |- (2.5,0) |- (A);
\end{tikzpicture}

See how the anchoring defines the start of the path from the node:

TODO angles

Not providing an anchor= or an angle= means that TiKZ will calculate the appropiate position automatically.

TODO unfinished! Will be posting more